本文来自微信民众号：中科院物理所（ID：cas-iop），作者：Marianne Freiberger，翻译：Nothing，校：loulou，标题图来自Unsplash

若是你在消息中看到有人胜利制作出了量子盘算机的话，你最好立时凝结本身的信用卡。因为，当你在网上购物时，现在一切珍爱你的信用卡信息的要领将会在几秒钟内被量子盘算机攻破。不光是你在银行内的信息，一切的加密信息在量子盘算机眼前都将被轻松破解。

网络平安依赖于一些很难处理的数学题目

关于量子盘算机有许多骇人听闻的说法，然则量子盘算机破解加密信息的超强才能是真的。现有的加密要领是基于那些用一般盘算机没法疾速处理的数学题目设想的，然则量子盘算机能够随意马虎攻破这类加密要领。那末量子盘算机另有哪些显着强于一般盘算机的妙技？

破译暗码

虽然为了回覆这个题目我们举办了许多理论方面的预备，然则这个题目依旧很顺手。RSA算法，一种普遍被用于珍爱信息平安的算法，它应用盘算机都很难疾速完成的因数剖析来举办加密。若是给你一个数字10，你立时就可以够告诉我它能够被剖析为2和5两个素数的乘积，然则若是我给你的数字是62615533，你应当没法经由过程默算告诉我它是哪些素数的乘积。

这不克不及见怪于你的默算才能。一旦数字足够大，盘算机也无计可施。“若是给出一个4000位的数字，即使是让现存的盘算机运转和宇宙岁数一样长的时候也没法将它剖析成一系列素数的乘积。”剑桥大学的量子盘算前驱Richard Jozsa说。

实在另有其他许多题目和剖析数字具有一样的特性：我们有许多能够处理它们的算法，然则跟着要处理的题目的难度的增添，所需算法的步数也越多。另一个有名的题目是旅行商题目，这个题目是说如何让旅行商接见每一个都市时所走的旅程最短：要接见的都市越多，题目越庞杂。

庞杂性理论依照处理题目的步数的增进速度来对种种题目举办分类。若是步数的增进是指数型的，好比旅行商题目，题目会变得非常顺手，因为指数型增进的增进速度会越来越快。当算法步数的增进跟着输入数字的增添显示成多项式情势时，我们才以为如许的题目是可处理的：若是输入的巨细是n，解题所需的步数正比于n²,n³或许n^k。虽然解题步数增进在我们看来照样很快（假定k=10），然则庞杂理论专家以为这类增进还算迟缓。“步数增进显示为多项式的数学模型是可盘算的，”Jozsa解释道，“若是步数增进不显示为多项式的情势，我们以为这类题目在现实操纵中是没法处理的。”

因数剖析被以为是弗成处理的题目：没有人写出能够由我们现在的盘算机运转的多项式时候（步数呈多项式型增进）算法。这恰是量子盘算能够大展神威的地方。1994年纪学家Peter Shor提出一种处理数字剖析题目的量子算法，它不光是多项式时候算法，而且k不大于3。这个算法应用数论的学问，将因数剖析题目转化成一种在特定的数学函数中辨认周期形式的题目——形式辨认恰是量子盘算机所善于的。

现在运用的其他加密算法也存在相似的题目，比方椭圆曲线加密算法（elliptic curve cryptography）：量子盘算机能够随意马虎破解它们。

这看起来量子盘算机有很大上风，但在这个领域内任何事情都是不确定的。“在庞杂性理论中，要证实给定的义务不克不及在多项式时候内处理是出了名的难题。”Jozsa说，“这是一个为难的现实。”因为没人晓得因数剖析的多项式时候算法，其实不意味着如许一个守候我们发明的算法不存在。“或许，下周能够就有一个智慧的数论专家把如许的算法找出来。” Jozsa说，“对量子盘算来讲，这有点失望。”

庞杂性题目

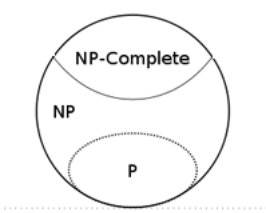
庞杂性的品级

关于其他题目状况如何？在其他的比因数剖析更难的题目中，量子盘算的威力会凌驾典范盘算吗？在回覆这个题目之前我们要明白“更难”的寄义，这把我们指导到了庞杂性类（complexity classes）的分级这里。起首引见“简朴的”题目，这类题目具有可在典范盘算机上运转的多项式时候算法，这类题目构成了一个被称为P的类。接下来是我们没有找到多项式时候算法的题目，但我们能够在多项式时候内来磨练解的正确性。这类题目被称为NP题目。因数剖析恰是属于这类题目。

在NP类题目中，有一些题目迥殊难明——这些题目被称为NP完整题目（NP-complete），旅行商题目属于这类题目。比NP完整题目越发庞杂的题目这里将不再引见。

因数剖析被归结于NP类题目但不属于NP完整题目。因为量子盘算能够在因数剖析题目中击败典范盘算，接下来的题目是，当触及NP完整题目时，量子盘算机显示如何？有一种说法以为，量子盘算机能够在眨眼之间处理NP完整题目。但这类说法过于乐观了。“我们不晓得我们是不是能够用量子盘算机处理NP完整题目，现实上，我们以为量子盘算机做不到这一点，”Jozsa解释道。

P和NP题目是一样庞杂的题目吗？

在这里，我们应当认识到庞杂性理论的核心题目：一切我们提到的器械都不克不及被证实。我们不只不晓得量子盘算机可否有效地处理NP完整题目，以至不晓得一般盘算机可否有效地处理这些题目。正如能够存在一个能够处理因数剖析题目但尚未被发明的多项式时候算法一样，也能够存在处理其他NP题目或NP完整题目的多项式时候算法。若是我们找到了这些算法，那末我们的庞杂性类条理的构造将会瓦解：P类、NP类和NP完整类将会属于统一类。若是你能证实或否认P类题目等价于NP类题目，那就厉害了，克莱数学研究所都邑嘉奖你一百万美圆：它被以为是数学中最风趣的七个开放题目之一。

量子盘算时机做甚么?

若是理论不是建立在坚固的基础上,那末我们如何包管量子盘算能够有现实用途呢？P题目在理论上是“轻易”处理的，然则你依然须要消费许多时候去处理它。这时候量子盘算机能够资助我们吗？

谜底是一定的。一个例子是“铁树开花”题目，它指的是从重大无纪律的数据库中找到特定的信息。试想，从包罗n个条目的电话号码簿中搜刮一个特定的号码而不是一个特定的名字。这是一个须要斲丧大批时候的义务，因为号码是无规则的，它不像名字一样是按纪律分列的。典范盘算机除一个一个的检索号码以外没有其他设施，最坏的状况是，我们发明电话号码簿中基础不存在我们要找的号码，或许这个号码处于末了一个地位，如许就须要举办n次操纵。而量子盘算机只须要n^0.5次操纵。这看起来并没有提速若干，然则当n足够大时，提速是相当可观的：以n=1000000为例，典范盘算机须要举办一百万次操纵而量子盘算机仅须要举办1000次操纵。

份子由大批遵照量子纪律的粒子构成

另一个量子盘算机能够大展技艺的领域是化学领域，生物和制药领域。若是你想明白一个份子体系，比方为了设想一种新药，一个明智的挑选就是在盘算机上模仿它的行动。难题在于份子是由许多粒子构成的，而这些粒子悉数遵照量子力学的纪律。我们晓得，跟着粒子数的增进，形貌份子体系所需的信息量呈指数增进，这使得盘算变得非常难题。“它具有指数级的庞杂性，”Jozas说，“只管是面临相对小的份子，最好的典范盘算机在模仿份子的量子动力学性子时也显得无计可施，但是量子盘算机能够胜任这项事情。”

暗码学也会受益于量子盘算机。比方，当量子态被观测时就会发作塌缩，应用这类性子能够监测信息是不是被其他人盗取。应用这类要领，人们能够给每一个人分发量子秘钥——一串能够用于对信息加密和解密的字符串。若是有人截获了秘钥我们立时就可以晓得。“这类器件之所以存在，是因为它们只须要几个量子比特，因而这属于量子手艺的领域。”Jozsa说。这类要领在2007年初次被用于大众实践，事先它被用来确保在瑞士日内瓦举办的推举中的选票平安转移。或许从理论的角度我们很难说量子盘算机具有甚么上风，然则最少我们晓得损坏我们的加密要领是要支付一些价值的。

原文地点：https://plus.maths.org/content/what-can-quantum-computers-do

本文来自微信民众号：中科院物理所（ID：cas-iop），作者：Marianne Freiberger，翻译：Nothing，校：loulou，标题图来自Unsplash

*文章为作者自力看法，不代表虎嗅网态度

本文由 中科院物理所© 受权 虎嗅网 宣布，并经虎嗅网编纂。转载此文请于文首标明作者姓名，连结文章完整性（包孕虎嗅注及其他作者身份信息），并请附上出处（虎嗅网）及本页链接。原文链接：https://www.huxiu.com/article/295719.html


未依照范例转载者，虎嗅保存追查响应义务的权益
将来眼前，你我还都是孩子，还不去下载 虎嗅App 猛嗅立异！,返回网站首页